Quasi static fracture simulations
Basic usage
The matscipy.fracture_mechanics.crack module provides classes and functions for setting up and analysing atomistic simulations of fracture.
The same functionality can be accessed in the command line interface, via the matscipy-quasistatic-fracture command.
import numpy as np
import ase.io
import ase.units as units
from ase.build import bulk
from ase.constraints import ExpCellFilter
from ase.optimize.precon import PreconLBFGS
from nglview import show_ase
from matscipy.fracture_mechanics.crack import CubicCrystalCrack
from matscipy.fracture_mechanics.clusters import diamond, set_groups
from matscipy.calculators.manybody.explicit_forms.stillinger_weber import StillingerWeber, Holland_Marder_PRL_80_746_Si
from matscipy.calculators.manybody import Manybody
/usr/lib/python3/dist-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.17.3 and <1.25.0 is required for this version of SciPy (detected version 1.26.4
warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"
We first setup a manybody calculator using the “inadvertendly modified Stillinger Weber” (IMSW) parameters, in which the strength of the 3-body potential was (initially accidentally) doubled. This is useful for us here as it gives a brittle fracture response.
calc = Manybody(**StillingerWeber(Holland_Marder_PRL_80_746_Si))
Bulk and Elastic properties
We can use this calculator to find the equilibrium lattice constant for bulk silicon by performing a variable cell relaxation using ExpCellFilter filter and PreconLBFGS optimizer from ASE. Since the cell is very small the preconditioning does not speed up the calculation; however, it is still useful as this is one of the most robust optimizers and it converges quickly. It is not necessary to use a cubic cell, we do it simply to make the calcualation of the cubic lattice constant alat straight-forward.
el = 'Si' # chemical element
si = bulk(el, cubic=True)
si.calc = calc
ecf = ExpCellFilter(si)
opt = PreconLBFGS(ecf)
opt.run(fmax=1e-6, smax=1e-6)
PreconLBFGS: 0 13:02:40 -34.692786 0.0000 0.0003
PreconLBFGS: 1 13:02:40 -34.692800 0.0000 0.0000
/tmp/ipykernel_8990/2868235177.py:4: FutureWarning: Import ExpCellFilter from ase.filters
ecf = ExpCellFilter(si)
/usr/local/lib/python3.10/dist-packages/ase/optimize/precon/lbfgs.py:133: UserWarning: The system is likely too small to benefit from the standard preconditioner, hence it is disabled. To re-enable preconditioning, call `PreconLBFGS` by explicitly providing the kwarg `precon`
warnings.warn('The system is likely too small to benefit from '
True
a0 = si.cell[0, 0]
Next we compute the elastic constants using matscipy.elasticity.fit_elastic_constants() assuming cubic symmetry to reduce the number of calculations required.
from matscipy.elasticity import fit_elastic_constants
si = bulk(el, a=a0)
si.calc = calc
C, C_err = fit_elastic_constants(si, symmetry='cubic')
Fitting C_11
Strain array([-0.02, -0.01, 0. , 0.01, 0.02])
Stress array([-4.18432088e+00, -2.05307995e+00, 2.76443651e-05, 1.97564777e+00,
3.87438786e+00]) GPa
Cij (gradient) / GPa : 201.46145206140295
Error in Cij / GPa : 2.6470858309107888
Correlation coefficient : 0.9997411341719054
Setting C11 (1) to 1.257423 +/- 0.016522
Fitting C_21
Strain array([-0.02, -0.01, 0. , 0.01, 0.02])
Stress array([-1.13681364e+00, -5.40617973e-01, 2.76443651e-05, 4.89093693e-01,
9.30336637e-01]) GPa
Cij (gradient) / GPa : 51.64012217253485
Error in Cij / GPa : 1.7644303723353547
Correlation coefficient : 0.9982534266249888
Setting C21 (7) to 0.322312 +/- 0.011013
Fitting C_31
Strain array([-0.02, -0.01, 0. , 0.01, 0.02])
Stress array([-1.13681364e+00, -5.40617973e-01, 2.76443651e-05, 4.89093693e-01,
9.30336637e-01]) GPa
Cij (gradient) / GPa : 51.640122172534916
Error in Cij / GPa : 1.7644303723352444
Correlation coefficient : 0.9982534266249891
Updating C31 (7) with value 0.322312 +/- 0.011013
Fitting C_44
Strain array([-0.02, -0.01, 0. , 0.01, 0.02])
Stress array([-2.43911453, -1.19994935, 0. , 1.16236259, 2.28858333]) GPa
Cij (gradient) / GPa : 118.17707663044219
Error in Cij / GPa : 1.285752128883671
Correlation coefficient : 0.9998224896711728
Setting C44 (4) to 0.737603 +/- 0.008025
[[b C11 b C12 b C12 b b b ]
[b C12 b C11 b C12 b b b ]
[b C12 b C12 b C11 b b b ]
[b b b b C44 b b ]
[b b b b b C44 b ]
[b b b b b b C44]]
=
[[201.46 51.64 51.64 0. 0. 0. ]
[ 51.64 201.46 51.64 0. 0. 0. ]
[ 51.64 51.64 201.46 0. 0. 0. ]
[ 0. 0. 0. 118.18 0. 0. ]
[ 0. 0. 0. 0. 118.18 0. ]
[ 0. 0. 0. 0. 0. 118.18]]
C_11 = 201.46 +/- 2.65 GPa
C_12 = 51.64 +/- 1.76 GPa
C_44 = 118.18 +/- 1.29 GPa
C_11 = C[0, 0] / units.GPa
C_12 = C[0, 1] / units.GPa
C_44 = C[3, 3] / units.GPa
We extract the cubic elastic constants \(C_{11}\), \(C_{12}\) and \(C_{44}\) and convert to units of GPa:
(C_11, C_12, C_44)
(201.46145206140295, 51.64012217253489, 118.17707663044219)
The remaining ingredient is the surface energy, which we can also compute on-the-fly
# UPDATE to import from here once `adapticecont` branch is merged.
# from matscipy.fracture_mechanics.clusters import find_surface_energy
def find_surface_energy(symbol,calc,a0,surface,size=(8,1,1),vacuum=10,fmax=0.0001,unit='0.1J/m^2'):
# Import required lattice builder
if surface.startswith('bcc'):
from ase.lattice.cubic import BodyCenteredCubic as lattice_builder
elif surface.startswith('fcc'):
from ase.lattice.cubic import FaceCenteredCubic as lattice_builder #untested
elif surface.startswith('diamond'):
from ase.lattice.cubic import Diamond as lattice_builder #untested
## Append other lattice builders here
else:
print('Error: Unsupported lattice ordering.')
# Set orthogonal directions for cell axes
if surface.endswith('100'):
directions=[[1,0,0], [0,1,0], [0,0,1]] #tested for bcc
elif surface.endswith('110'):
directions=[[1,1,0], [-1,1,0], [0,0,1]] #tested for bcc
elif surface.endswith('111'):
directions=[[1,1,1], [-2,1,1],[0,-1,1]] #tested for bcc
## Append other cell axis options here
else:
print('Error: Unsupported surface orientation.')
# Make bulk and slab with same number of atoms (size)
bulk = lattice_builder(directions=directions, size=size, symbol=symbol, latticeconstant=a0, pbc=(1,1,1))
cell = bulk.get_cell() ; cell[0,:] *=2 # vacuum along x axis (surface normal)
slab = bulk.copy() ; slab.set_cell(cell)
# Optimize the geometries
from ase.optimize import LBFGSLineSearch
bulk.calc = calc ; opt_bulk = LBFGSLineSearch(bulk) ; opt_bulk.run(fmax=fmax)
slab.calc = calc ; opt_slab = LBFGSLineSearch(slab) ; opt_slab.run(fmax=fmax)
# Find surface energy
import numpy as np
Ebulk = bulk.get_potential_energy() ; Eslab = slab.get_potential_energy()
area = np.linalg.norm(np.cross(slab.get_cell()[1,:],slab.get_cell()[2,:]))
gamma_ase = (Eslab - Ebulk)/(2*area)
# Convert to required units
if unit == 'ASE':
return [gamma_ase,'ase_units']
else:
from ase import units
gamma_SI = (gamma_ase / units.J ) * (units.m)**2
if unit =='J/m^2':
return [gamma_SI,'J/m^2']
elif unit == '0.1J/m^2':
return [10*gamma_SI,'0.1J/m^2'] # units required for the fracture code
else:
print('Error: Unsupported unit of surface energy.')
surface_energy, unit = find_surface_energy(el, calc, a0, 'diamond111')
Step Time Energy fmax
LBFGSLineSearch: 0 13:02:40 -416.313600 0.000000
Step Time Energy fmax
LBFGSLineSearch: 0 13:02:40 -403.303800 0.000002
Build crack system
We now have all the material parameters needed and can proceed to define the crack system. Usually the contents of the cell below (together with the code above to compute the elastic constants and surface energy) would be included in a file named params.py which would then be imported by the scripts in matscipy/fracture_mechanics/scripts, e.g. the quasistatic_crack.py script on which this tutorial is based.
n = [ 4, 4, 1 ]
crack_surface = [ 1, 1, 1 ]
crack_front = [ 1, -1, 0 ]
crack_tip = [ 41, 56 ]
skin_x, skin_y = 1, 1
vacuum = 6.0
fmax = 0.05
# Setup crack system
cryst = diamond(el, a0, n, crack_surface, crack_front)
set_groups(cryst, n, skin_x, skin_y)
ase.io.write('cryst.cfg', cryst)
# Compute crack tip position
r0 = np.sum(cryst.get_positions()[crack_tip,:], axis=0)/len(crack_tip)
tip_x0, tip_y0, tip_z0 = r0
skin_x = 1*a0, skin_y = 1*a0
skin_x = 6.651528492212671, skin_y = 9.406681804198225
We can now visualise the crystall unit cell:
show_ase(cryst)
We define a CubicCrystalCrack object to represent our crack system. This takes the crystal orientations and the elastic constants (either as three cubic constant as we do here, or as a full 6x6 stiffness matrix in either the crystal reference frame or rotated to the specimen frame).
crk = CubicCrystalCrack(crack_surface, crack_front,
C_11, C_12, C_44)
By providing the surface energy, the crk object can be used to compute the Griffith estimate of the critical stress intensity factor at which fracture becomes thermodynamically favourable.
k1g = crk.k1g(surface_energy)
k1g
137.72126045164697
Apply initial strain field
We have everything we need to apply the continuum linear elastic displacement field to our crystal. We centred the field on the middle of the cryst structure.
tip_x = cryst.cell.diagonal()[0]/2
tip_y = cryst.cell.diagonal()[1]/2
crack = cryst.copy()
crack.set_pbc([False, False, True])
k1 = 1.0
ux, uy = crk.displacements(cryst.positions[:,0], cryst.positions[:,1],
tip_x, tip_y, k1*k1g)
crack.positions[:, 0] += ux
crack.positions[:, 1] += uy
# Center notched configuration in simulation cell and ensure enough vacuum.
oldr = crack[0].position.copy()
crack.center(vacuum=vacuum, axis=0)
crack.center(vacuum=vacuum, axis=1)
tip_x += crack[0].x - oldr[0]
tip_y += crack[0].y - oldr[1]
show_ase(crack)
import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.scatter(cryst.positions[:,0], cryst.positions[:,1], s=50, c=cryst.arrays['groups'])
ax1.quiver(cryst.positions[:,0], cryst.positions[:,1], ux, uy)
ax2.scatter(cryst.positions[:,0] + ux, cryst.positions[:,1] + uy, s=50, c=cryst.arrays['groups'])
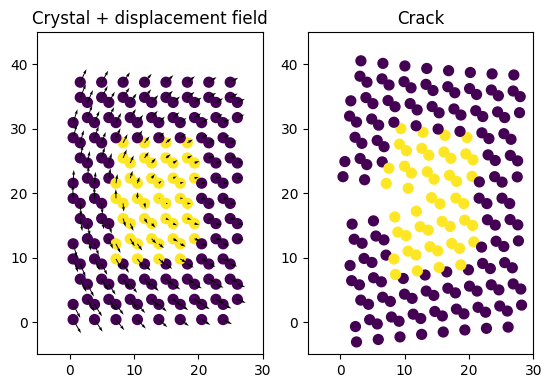
ax1.set_title('Crystal + displacement field')
ax2.set_title('Crack')
for ax in [ax1, ax2]:
ax.set_aspect('equal')
# ax.set_xticks([])
# ax.set_yticks([])
ax.set_xlim(-5, 30)
ax.set_ylim(-5, 45)
pass
