Nested sampling method¶
- Authors:
Noam, Rob, Gabor, Livia
- Date:
2015
Overview¶
The nested sampling method was first introduced by John Skilling [1] in the field of applied probability and inference to efficiently sample probability densities in high-dimensional spaces where the regions contributing most of the probability mass are exponentially localized. It is an annealing algorithm that creates a sequence of probability distributions, each more concentrated than the previous one near the high-likelihood region of the parameter space - i.e. in the context of materials, the low-energy region of configuration space.
Since its original inception, nested sampling has also been applied to atomistic systems, and its several advantages mean it became a powerful method to sample atomic configuration spaces.[#f2]_ * calculate the partition function, hence all thermodynamic properties become accessible
calculate the heat capacity and locate the phase transitions
with an order parameter calculate the free energy
the sampling process itself is independent of temperature, thus the calculation of thermodynamic quantities is a simple post-processing step
no prior knowledge is needed of the phases or phase transitions
can be used with both constant volume and constant pressure calculations
calculate the entire phase diagram in an automated way
considerable computational gain over parallel tempering
Publications¶
L.B. Partay, A.P. Bartok, G. Csanyi, Efficient Sampling of Atomic Configurational Spaces, J. Phys. Chem. B (2010), 114, 10502–10512, https://pubs.acs.org/doi/abs/10.1021/jp1012973
R.J.N. Baldock, L.B. Partay, A.P. Bartok, M.C. Payne, G. Csanyi, Determining pressure-temperature phase diagrams of materials, Phys. Rev. B (2016), 93, 174108, https://journals.aps.org/prb/abstract/10.1103/PhysRevB.93.174108
R.J.N. Baldock, N. Bernstein, K. M. Salerno, L.B. Partay, G. Csanyi, Constant-pressure nested sampling with atomistic dynamics, Phys. Rev. E (2017), 96, 043311, https://link.aps.org/doi/10.1103/PhysRevE.96.043311
L.B. Partay, G. Csanyi and N. Bernstein Nested sampling for materials, Eur. Phys. J. B (2021) 94, 159, https://link.springer.com/article/10.1140/epjb/s10051-021-00172-1
Further examples of publications using the pymatnest package:
L.B. Partay On the performance of interatomic potential models of iron: Comparison of the phase diagrams, Comp. Mat. Sci. (2018), 149, 153, https://www.sciencedirect.com/science/article/pii/S0927025618301794
J. Dorrell, L.B. Partay Thermodynamics and the potential energy landscape: case study of small water clusters, Phys. Chem. Chem. Phys. (2019), 21, 7305 https://pubs.rsc.org/en/content/articlehtml/2019/cp/c9cp00474b
A.P. Bartok, G. Hantal and L.B. Partay Insight into Liquid Polymorphism from the Complex Phase Behavior of a Simple Model, Phys. Rev. Lett. (2021) 127, 015701 https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.015701
L.B. Partay and G. Hantal Stability of the high-density Jagla liquid in 2D: sensitivity to parameterisation, Soft Matter, (2022) 18, 5261 https://pubs.rsc.org/en/content/articlelanding/2022/SM/D2SM00491G
M. Yang, L.B. Partay and R.B. Wexler Surface phase diagrams from nested sampling, Phys. Chem. Chem. Phys., (2024),26, 13862, https://pubs.rsc.org/en/content/articlehtml/2024/cp/d4cp00050a
Algorithm¶
Nested sampling is an iterative, “top-down” method, it samples the Potential Energy Landscape (PES) through a series of nested energy levels, starting from the high energy region (gas phase) and going towards the global minimum. The sampling is done using a set of walkers - these are randomly generated configurations at the initial step of the sampling, and the number of these determine the “resolution” of which the PES is sampled. Then, at every iteration step, the walker with the highest energy (enthalpy in case of constant pressure sampling) is removed, and a new one is generated to keep the number of walkers constant. To generate the new configuration, one of the existing walkers is randomly selected and cloned, and this cloned configuration is modified (through an MCMC, a total-enthalpy Hamiltonian MC or a Galilean MC walk), such that its energy (enthalpy) does not exceed the that of the last removed walker. The iteration is continued until a satisfactory low energy configuration is reached.
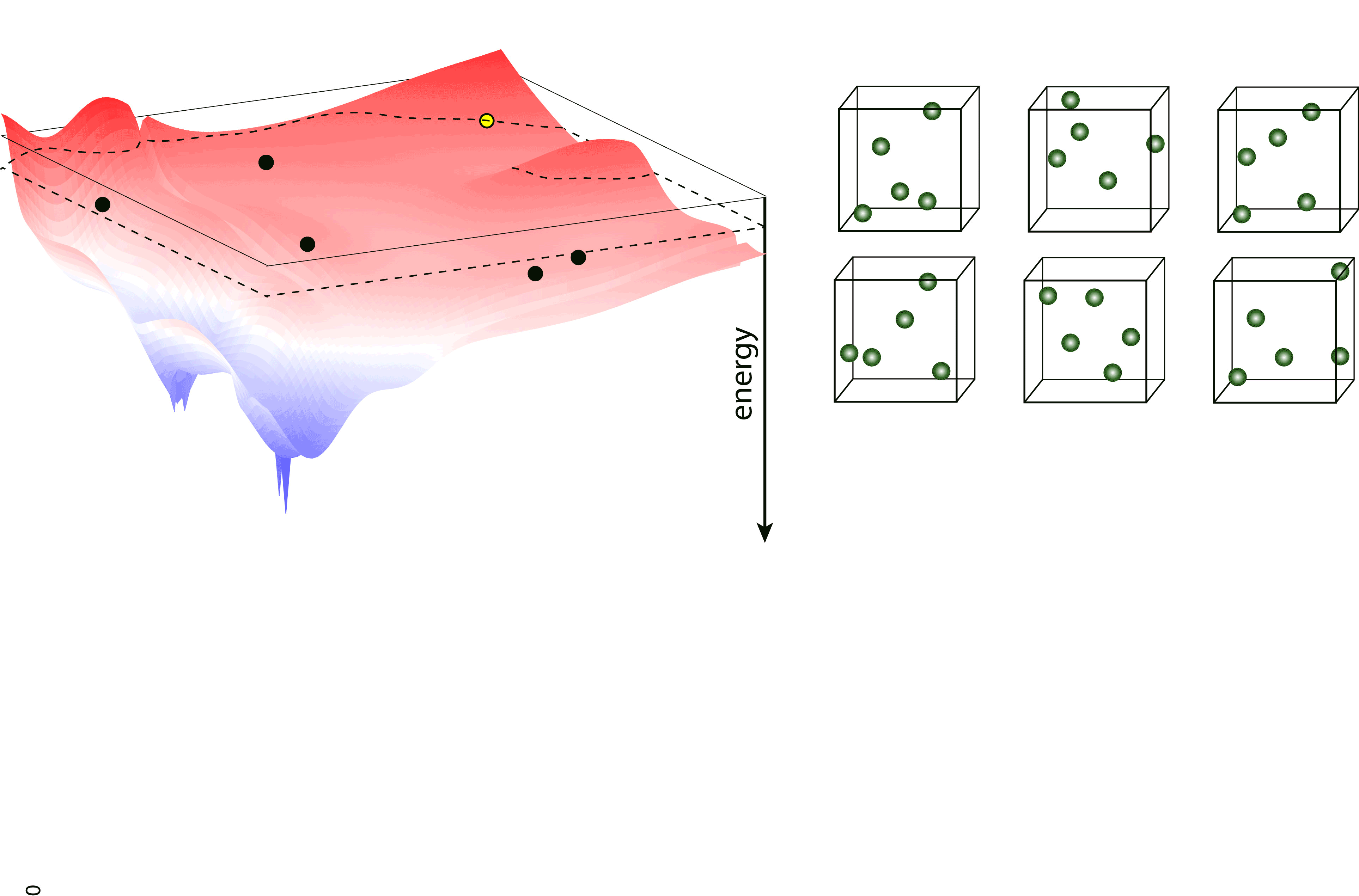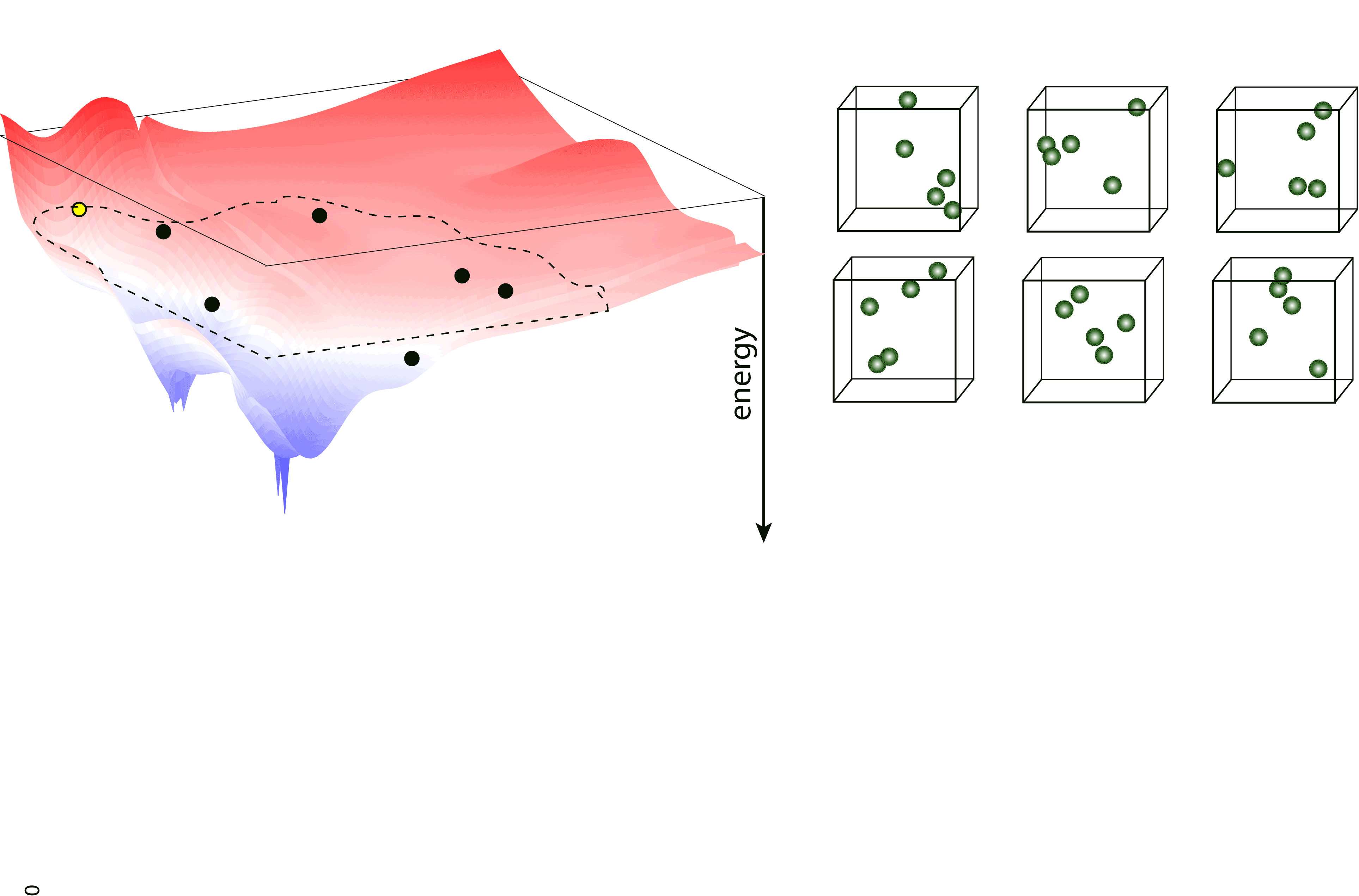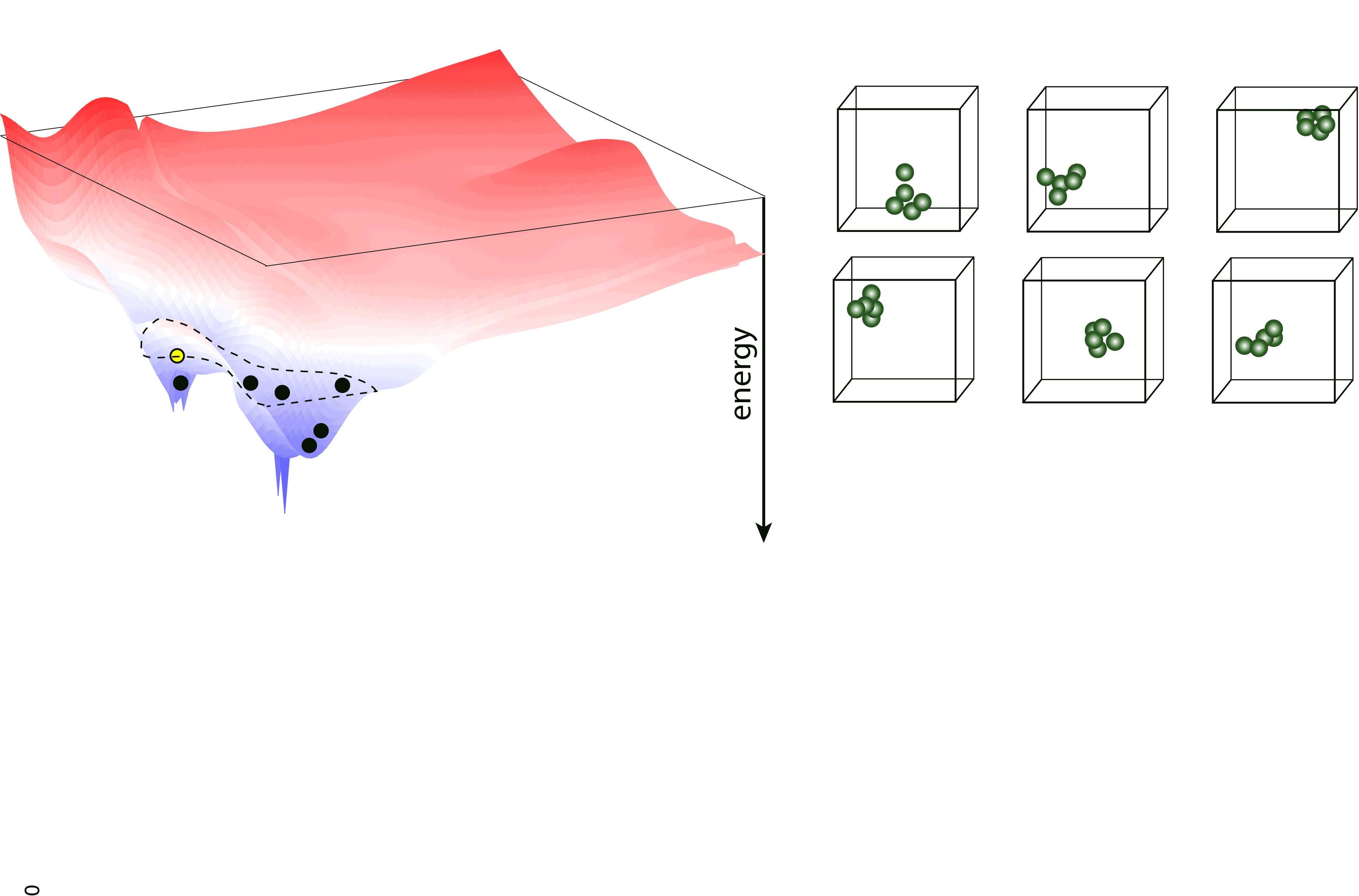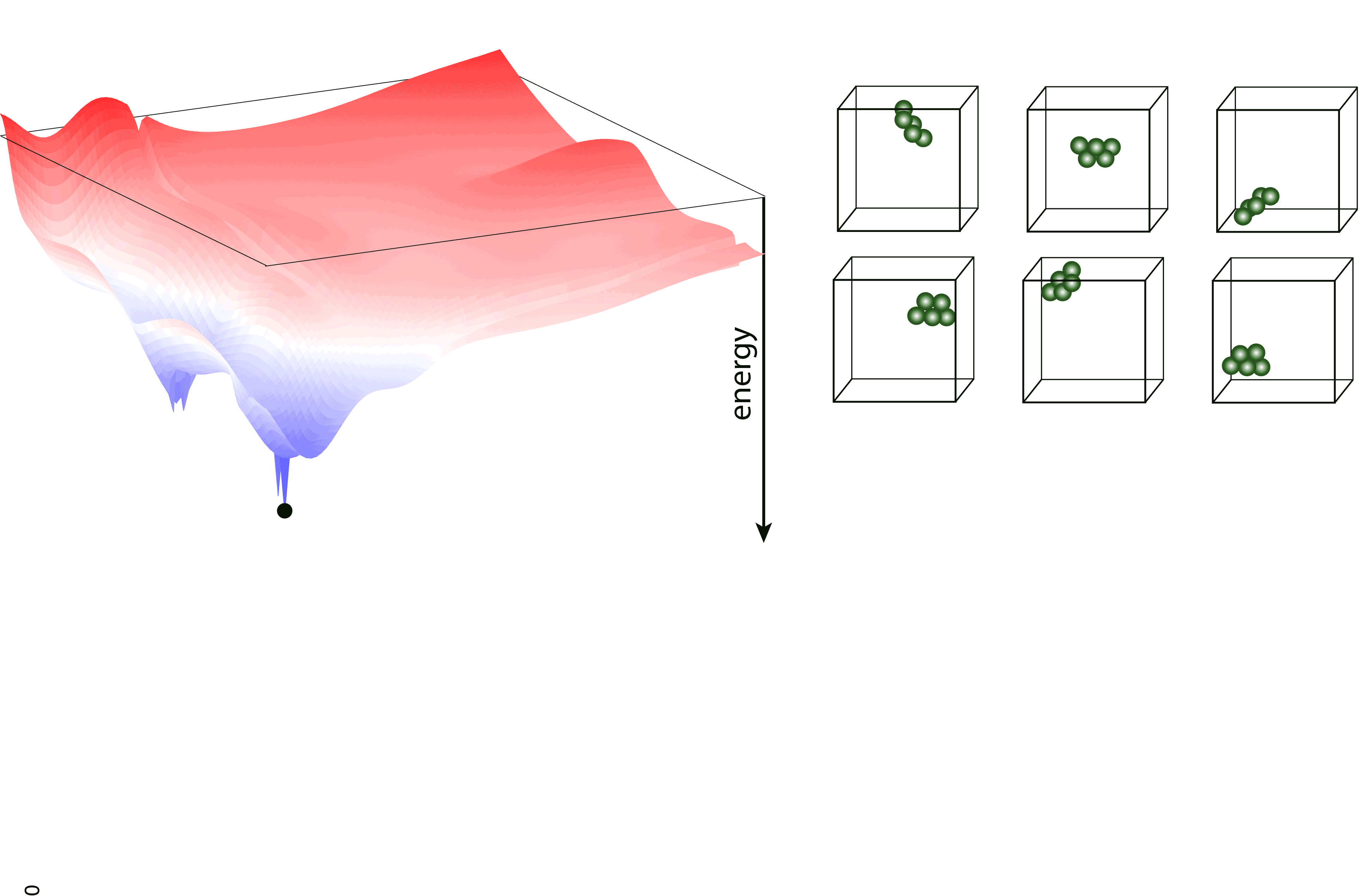
pymatnest¶
The pymatnest package is a software
library written in Fortran 95/python for the purpose of carrying out
nested sampling calculations with a variety of options suitable for different systems.
It can be used with the supplied fortran potential models and it also has interfaces with the following packages:
LAMMPS
MC and MD step algorithms¶
rej_free_perturb_velo- if atom_velo_rej_free_fully_randomize:
pick random velocities consistent with Emax
- else: (perturb velocities)
- if current velocity=0:
can’t rescale, so pick random velocities consistent with Emax
- else:
pick new random magnitude consistent with Emax, random rotation of current direction with angle uniform in +/- atom_velo_rej_free_perturb_angle
do_MC_atom_velo_walk- if MC_atom_velo_walk_rej_free:
call rej_free_perturb_velo()
- else:
do MC pertubation to velocities
do_MD_atom_walk- if MD_atom_velo_pre_perturb:
call do_MC_atom_velo_walk() for magnitude and rotation
propagate in time atom_traj_len time steps of length MD_atom_timestep
- if MD_atom_reject_energy_violation is set:
accept/reject entire move on E deviating by less than MD_atom_energy_fuzz times kinetic energy
accept/reject entire move on E < Emax and KE < KEmax
- if reject
set positions, velocities, energy back to value before perturbation (maybe should be after?)
- else: (accepted)
- if MD_atom_velo_flip_accept:
flip velocities
- if MD_atom_velo_post_perturb:
call do_MC_atom_velo_walk() for magnitude and rotation
do_MC_atom_walk- if MC_atom_velocities and MC_atom_velocities_pre_perturb:
call do_MC_atom_velo_walk() to perturb velocities, magnitude and rotation
- if using fortran calculator and not reproducible:
call fortran MC code f_MC_MD.MC_atom_walk
- else: (do python MC)
- if MC_atom_Galilean:
go Galilean MC in python
- else:
- loop atom_traj_len times
- loop over atoms in random order
propose single atom move
accept/reject on E < Emax
do_MC_swap_step- if all atomic numbers are identical:
return
randomly pick a desired cluster size
pick two clusters with distinct atomic numbers, backing off to smaller clusters on failure to find appropriate larger clusters, but always pick at least a pair of atoms to swap
- if energy < Emax:
accept swap
do_MC_cell_volume_step
do_MC_cell_shear_step
do_MC_cell_stretch_step
do_atom_walkloop n_atom_steps_per_call times, calling do_MC_atom_walk() or do_MD_atom_walk()
walk_single_walker- loop while n_model_calls_used < n_model_calls:
- pick random item from list:
do_atom_walk n_atom_step_n_calls
do_cell_volume_step n_cell_volume_steps
do_cell_shear_step n_cell_shear_steps
do_cell_stretch_step n_cell_stretch_steps
do_swap_step n_swap_steps
do_semi_grand_step n_semi_grand_steps
do move
perturb final energy by random_energy_perturbation
full_auto_set_stepsizesStep sizes for each (H)MC move are set via a loop which performs additional exploration moves, calibrating each step size to obtain an acceptance rate inside a specified range.
The routine is MPI parallelised, so that the wall time goes as 1/num_of_processes
For each (H)MC move type the following is performed:
Set
movement_argsparameters so that only one (H)MC call is made at a timeMin and max acceptance rates are copied from parameters MC_adjust_min_rate / MD_adjust_min_rate and MC_adjust_max_rate / MD_adjust_max_rate
- loop for step size calibration, repeat the following 200/num_of_MPI_processes times:
Copy a configuration from the live set (each MPI process chooses a different configuration)
Each MPI processes performs one (H)MC move on its cloned configuration
running statistics for the number of accepted/rejected moves on each process are recorded
The total number of accepted/rejected moves for this step size (summed across all MPI processes) are estabilshed
- if the total acceptance rate is within the desired range:
return this stepsize
- else:
- if this is not the first time the loop has been performed for this (H)MC move and we previously obtained an acceptance rate on one side of the desired range:
now find an acceptance rate on the other side of the desired range
return the step size that gave an acceptance rate closest to the middle of the desired range.
- else: (this is the first time)
Store step length and acceptance rate
update step length, by or by MC_adjust_step_factor, to improve acceptance rate
Check that step size is not larger than max allowed value (specified by user), and also that step size is not smaller than 10-20(useful for detecting errors).
return step sizes and time taken for routine to run
main: parse arguments- process n_atom_steps
- if break_up_atom_traj:
n_atom_steps_per_call = 1
n_atom_steps_n_calls = n_atom_steps
- else:
n_atom_steps_per_call = n_atom_steps
n_atom_steps_n_calls = 1